How to Escape the Hyperclassical Trap

From its outset, the modern classical education movement has been primarily conceived as a reaction against the powerful progressive forces that shape our current educational landscape. Many of the foundational philosophical books in classical education begin with a chapter titled something like “Our Education Crisis” or “The Loss of Learning” or “The Failure of Modern Education” and proceed to deliver a scathing indictment of the practices and products of contemporary progressive education.

In Douglas Wilson’s Recovering the Lost Tools of Learning, our educational system is “morally bankrupt,” having been undergirded with “false philosophy;”¹ in Gene Veith and Andrew Kern’s Classical Education: The Movement Sweeping America, progressive education “creates a sense of helplessness and dependence” breeding an “ignorance that leads to vice” which leads to the “disintegration of culture;”² and, most contemptuously, in David Hicks’s Norms and Nobility, the modern educational system is “built to accommodate near-morons” and “makes near-morons of everyone in the system.”³ Many of the criticisms in these chapters are more than justified; still, the inflammatory language necessarily positions classical education as an opposing extreme to the progressive status quo.

The Plague of Hyperclassical Education

On the one hand, this reactionary character of classical education seems quite natural, as any movement that purposes to be a recovery (or in Stratford Caldecott’s words a “ressourcement”⁴) must necessarily derive its purpose from some societal departure or drift. There are numerous ideals within progressivism – like the sociocultural disintegration of objective truth – that deserve an extreme reaction and drive classical education to some of its most fundamental principles – like a logocentric understanding of knowledge.

On the other hand, however, especially in the realm of pedagogy, the classical education movement faces a crisis itself since it defines itself by what it stands against rather than what it stands for. Consider the common phrases used by headmasters as they give tours of classical schools: “our students don’t spend all their time in front of screens,” “the desks aren’t grouped together for project-based learning,” or “you won’t see any smart boards or goofy posters on the walls.” Consider the dearth of books or articles written with any kind of positive vision for classical pedagogy. And, most egregiously, consider the soul-sucking commitment to strictness and rigor, the imagination-stifling lack of creativity, and the dogmatic refusal to consider anything outside of direct instruction that have come to define “classical” teaching in many of our schools.

While I have no desire to promote excessive group work or a one-to-one device-to-student ratio, it has become quite clear that our supposedly classical pedagogy has overreacted against progressivism and become something better termed “hyperclassical.” This hyperclassical instruction, which is characterized by an overreliance on lecture, a commitment to repetition and drill, and a fundamental lack of wonder, inquiry, and exploration, certainly represents a departure from the dangers of progressivism, but rather than providing the framework for a classical recovery of the true, good, and beautiful, it instead has come to represent an equally dangerous extreme of its own.

The Hyperclassical Math Classroom

As an illustration of the difference between classical and hyperclassical pedagogy, consider the mathematics teaching found in most classical schools. Mathematics is (and has always been) a subject that reveals pedagogy – while there may be slight differences in curricula, for the most part, every school in the country teaches fractions, word problems, solving for x, and the quadratic formula. In a discipline such as literature, the statement that “our students read Crime and Punishment instead of The Hunger Games” can provide a curricular response⁵ to what makes classical education distinctive; in mathematics, however, it must be the pedagogy – that is, the ways in which teachers engage students in learning, the structure and content of classroom conversations, the kinds of relationships that are encouraged and drawn upon, and the nature of the questions that are asked and answered – that sets the classical classroom apart.

Yet, our mathematics pedagogy is woefully off-base, having succumbed to hyperclassical principles. Reacting against the progressive tendency to downplay algorithms and procedures in favor of conceptual understanding, hyperclassical teaching doubles down on the building of skills, compelling students to memorize and regurgitate mathematical facts and formulas. Reacting against the progressive tendency to eliminate things like homework, showing your work, and even right answers, hyperclassical teaching relies on practice, repetition, and perfection as the primary pedagogical driver, often prescribing upwards of twenty-five practice problems a night for homework.⁶

And, reacting against the progressive tendency to emphasize inquiry, project-based learning, and group work, hyperclassical teaching relies heavily on the instructor to explain, boil down, and parse out all the details of the day’s lesson. Where progressivism has become soft and relativistic, hyperclassicalism has become hard and unforgiving. Where progressivism has become critical, hyperclassicalism has become dogmatic. Where progressivism has become entirely student-centered, hyperclassicalism has become completely teacher-driven. But neither of these extremes can provide a genuine vision for pedagogy that values both truth and the discovery of truth, that partners the teacher and student together in the educational enterprise, and that seeks to combine experience and expertise to stimulate and cultivate the moral imagination.

Euler’s Bridge to Wonder

To illustrate just how far this hyperclassical pedagogy has strayed from classical principles, walk for a few minutes in the footsteps of the greatest mathematician who ever lived: Leonhard Euler.⁷ In 1735, Euler was living in St. Petersburg when he came across a story from the nearby Prussian city of Königsberg (now Kaliningrad, Russia). Königsberg is located on the Pregolya River, which not only divides the city in half but splits and reconnects forming an island and a peninsula (Figure 1). According to legend, the citizens of Königsberg would wander around the city on Sunday afternoons trying to invent a route that would allow them to cross each of the seven bridges in the town exactly once.⁸

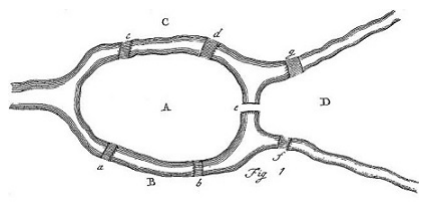
Hearing the story, Euler was intrigued; a few moments with the problem is enough to see that such a route is impossible, but Euler continued to wonder at the puzzle, writing to a friend, “This question is so banal, but seemed to be worthy of attention in that neither geometry, nor algebra, nor even the art of counting was sufficient to solve it.”⁹

Later that year, Euler presented a paper with a proof of the Königsberg bridge problem, complete with new mathematical ideas that could be used to arrive at a solution.¹⁰ To simplify matters, Euler modeled Königsberg with a connected graph (Figure 2) in which the landmasses (A, B, C, and D) were represented by points (called vertices) and the bridges (a, b, c, d, e, f, and g) were represented by lines (called edges).¹¹ With the clarity provided by the graph, Euler is not only able to solve the bridge problem for the city of Königsberg, but he provides a formula for determining if a route is possible for any city: 

In any connected graph, it is possible to find a path that traverses each edge exactly once if and only if there are no more than two vertices that have an odd number of edges attached.

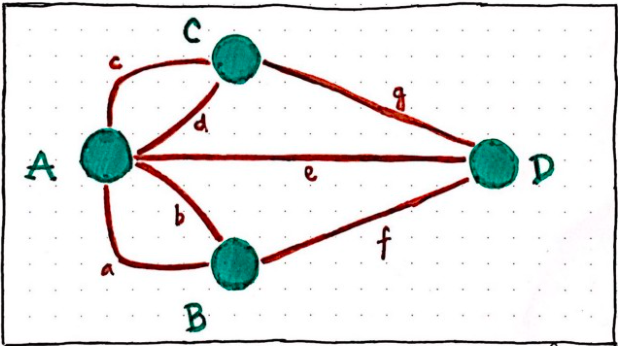
Here, Euler recognizes the problem with Königsberg – every landmass has an odd number of entry and exit points and thus, since you need to use two bridges to arrive and depart from a landmass, when there is only one bridge remaining, a walker would be stranded on that landmass forced to re-use a bridge to leave.

For example, consider the island A: in the course of the walk, you might use bridge c to arrive and bridge d to depart and then (after walking across bridge g) use bridge e to arrive and bridge a to depart; but this leaves bridge b as problematic because you would have to cross it at some point which would leave you stranded on the island, since there would no longer be any uncrossed bridges connected to A. Such “strand-able” locations are not in-and-of-themselves problematic as long as they are either the starting and ending point of the walk (for example, consider that the graph in Figure 3 where bridge c is removed does have a possible route as long as you start and end at B or D). With four odd vertices, however, Königsberg has too many strand-able locations, and thus the seven bridges cannot be crossed exactly once.

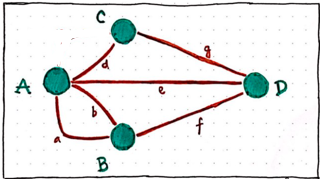
This a singular moment of brilliance from Euler, providing the solution to a complex problem, and this seemingly unremarkable paper launched an entire field of mathematics that has come to be known as graph theory. On the heels of the Königsberg bridge problem, a number of other related questions quickly emerge: which graphs allow you to cross each bridge exactly once while starting and finishing at the same spot (an Eulerian cycle); which graphs allow you to visit each vertex exactly once (a Hamiltonian path); if each bridge has a toll, what is the cheapest route that visits each vertex exactly once (the travelling salesman problem). As these problems are explored and solved, graph theory gradually expands to include not only other route problems but other topologies and other kinds of networks as well.

Towards a Pedagogy of Wonder

So, what does this walk in Euler’s footsteps teach us about classical pedagogy? Consider the progression that Euler follows as he encounters, re-imagines, and solves the Königsberg bridge problem. First, he begins in wonder; that is, he comes face-to-face with a natural dilemma in the world and finds himself completely absorbed in the problem – his imagination captivated and his intellect inspired. Second, he explores the situation, applying a mathematical lens to represent the situation with a quantitative model. Third, he solves the problem, persevering until he is satisfied not only with his answer but also his explanation. Finally, he generalizes his answer, creating a formula that synthesizes the patterns he has discovered and applies more universally to other as-yet-unsolved problems. This, in turn, returns him to wonder once more, as it opens up further questions to consider and deeper mysteries to probe.

Given the centrality of this progression in characterizing the thinking of the great mathematicians, it seems natural that a similar progression – from wonder to exploration to solving to generalizing and back to wonder – should be woven into the way we teach students.¹² Yet, as we have swung towards hyperclassicalism, rather than fix the problems of progressive education, our instruction often follows the exact opposite sequence to the process we see modeled by Euler: we begin by providing students with a generalization or formula, then turn them loose on a set of practice problems to solve, and only then (if at all) incorporate any kind of exploration or wonder. We drill formulas into our students’ heads, give them a multitude of problems to solve, try to shoehorn a mathematical model or pictorial representation in to explain the algorithms, and then expect them to be somehow moved or inspired by this wonder-less-ness.

Paul Lockhart, in his brilliant essay “A Mathematician’s Lament” says it best:

Mathematics is the art of explanation. If you deny students the opportunity to engage in this activity — to pose their own problems, make their own conjectures and discoveries, to be wrong, to be creatively frustrated, to have an inspiration, and to cobble together their own explanations and proofs — you deny them mathematics itself. So no, I’m not complaining about the presence of facts and formulas in our mathematics classes, I’m complaining about the lack of mathematics in our mathematics classes.¹³

We have, through our hyperclassical pedagogy, truly denied our students mathematics itself.

True Classical Education

In place of this hyperclassical inversion, classical pedagogy must, in true Aristotelian fashion, seek the mean between these two extremes, not merely standing against progressivism, but standing for some positive middle ground. As we see in the example of Euler, this middle ground must be rooted in a pedagogical progression that begins with wonder, where teachers pose genuine questions to students, encourage them to experience dilemmas in the world around them, engage their imaginations, let them struggle, elicit their opinions, and entertain a multitude of potential ideas.

These experiences and opinions are not the end goal of pedagogy (as might be the case in a progressive classroom), but they help to instill a sense of wonder and a depth of inquiry in the student and provide a foundation for the teacher to lead an authentic classroom discussion. Using wonder as the catalyst, the teacher can then ask a series of questions that begin to prune the variety of opinions, separating the right from the wrong, and arriving, finally, at a generalizable and universal truth. Classical education’s commitment to logocentricism does not mean that truth should be force-fed to students. Rather, students must encounter truth, they must wonder about it, and they must defend it against its alternatives in order for it to become something that they finally know and love.

This wonder-based pedagogy can at times be uncomfortable, especially for teachers. Notice that wonder, both in the case of Euler and for all of us, takes on a double meaning – that of beholding or appreciating something sublime as well as that of questioning or speculating at something unknown. Promoting wonder in students, then, given its link to the unknown, feels dangerous to teachers, especially those accustomed to a hyperclassical modus operandi, as a potential threat to their authority in the classroom.

A pedagogy of wonder requires teachers to embrace what is unfamiliar, undiscovered, and mysterious, posing genuine questions, not as some sort of inconsequential academic game (as progressive pedagogy might do) nor as a systematic chopping up of truth into bite-sized pieces (as would be the case in hyperclassicalism), but as an authentic “launch[ing] into the deep,”¹⁴ as Annie Dillard puts it, in the hopes of catching some glimpse of the sublime amidst the unknown. A teacher’s real authority in the classroom does not come from having all of the answers to a carefully controlled and curated set of questions that stifle curiosity; rather, it comes from admitting that wonder often lies beyond our understanding and humbly leading the pursuit of the wonderous amidst that which is unfamiliar to teacher and student alike.

Carving out this via media is by no means an easy task. Aristotle recognizes as much in his Ethics as he articulates the difficulties of hitting the mean between extremes: “It is easy to miss the target but hard to hit it… Excess and deficiency characterize vice, while the mean characterizes virtue: for ‘bad men have many ways, good men but one.’”¹⁵ Yet if classical education does indeed intend to live up to its moniker of “classicus” (the best), it must not shirk this difficult work. It must resist the temptation to react wildly to the progressive forces, but must instead establish, slowly and intentionally, a middle pedagogical ground between the Scylla of progressivism and the Charybdis of hyperclassicalism, a truly classical pedagogy that begins and ends in wonder.

Jonathan Gregg is a Visiting Assistant Professor of Education at Hillsdale College, regularly teaching classes including The Classical Quadrivium, Mathematics and Deductive Reasoning, Logic & Rhetoric, and Teaching Secondary Mathematics. He has a B.A. in Mathematics and English from Hillsdale College, an M.A. in Humanities from the University of Chicago, and is currently pursuing a PhD in Mathematics Education from Michigan State University. Previously, he served as an Assistant Director of Hillsdale College’s Barney Charter School Initiative, and he has also taught middle/high school mathematics in the Great Hearts charter school system. His research interests center around the teaching and learning of mathematics in classical schools, Socratic pedagogy, Singapore mathematics, the educational philosophy of Martin Buber, and the classical quadrivium. He lives in Hillsdale with his wife, Casey, and their two children, Eliana (4) and Simeon (1).

This is the second essay in our symposium, “The Future of Classical Education.” See the introduction and a list of all the essays here.

1. Wilson, Douglas. Recovering the lost tools of learning: An approach to distinctively Christian education. Vol. 12. Crossway, 1991. p. 142.
2. Veith, Gene Edward, and Andrew Kern. Classical education: The movement sweeping America. Vol. 30. Capital Research Center, 2001. p. 10.
3. Hicks, David V. Norms & nobility: A treatise on education. Rowman & Littlefield Pub Incorporated, 1991. p. 148.
4. Caldecott, Stratford. Beauty for truth’s sake: On the re-enchantment of education. Brazos Press, 2017. p. 13.
5. Albeit a somewhat poor response.
6. Saxon Math’s [in]famous instruction to the student in the introduction to each textbook comes to mind: “Remember, solve every problem in every practice set.”
7. While admittedly a subjective opinion, few mathematicians other than Gauss can match Euler for breadth, ingenuity, and lasting contributions to the field, as he published more than 500 books and papers in his lifetime.
8. I owe much of my knowledge of this story to Teo Paoletti’s excellent research report on the subject, published by the MAA: Teo Paoletti (The College of New Jersey), “Leonard Euler’s Solution to the Konigsberg Bridge Problem,” Convergence (May 2011).
9. Quoted in: Hopkins & Wilson. “The Truth about Königsberg.” College Mathematics Journal (2004), 35, 198-207.
10. Euler, Leonhard, ‘Solutio problematis ad geometriam situs pertinentis’ (1741), Eneström 53, MAA Euler Archive.
11. Figure 2 appears online at: https://medium.com/basecs/k%C3%B6nigsberg-seven-small-bridges-one-giant-graph-problem-2275d1670a12.
12. After all, what are we trying to form in our mathematics classes, if not mathematicians? Though numerous teachers and textbooks are intentional about using the word “mathematicians” to describe students, few have put any thought into how a student might be encouraged to develop into one, transforming those good intentions into mere lip service that fails to provide any concrete pedagogical solutions.
13. Lockhart, Paul. A mathematician’s lament: How school cheats us out of our most fascinating and imaginative art form. Bellevue literary press, 2009. p. 3.
14. Dillard, Annie. Pilgrim at Tinker Creek. Harper and Row, 1974. p. 33.
15. Aristotle. The Nicomachean Ethics, trans. Martin Ostwald. Pearson, 1999. p. 43, 1106b, 30.